अनंत विस्तार की आवेशित समतल पतली अचालक शीट के कारण विद्युत क्षेत्र की तीव्रता (electric field due to a charged thin non - conducting sheer of infinite extent):-

         आवेशित सीट के निकटवर्ती विन्दुओं पर विद्युत क्षेत्र की तीव्रता:-

electric field due to non conducting sheet in hindi, Gauss law application in hindi,
         माना एक पतली आवेशित चालक thin charge conducting sheet सीट जो कि एक समान रुप से आवेशित हो, इसके प्रति एकांक पृष्ठ पर आवेश घनत्व (Charge density per unit area) है। 
               इसके प्रति एकांक पृष्ठ पर आवेश को पृष्ठ आवेश घनत्व surface charge density कहते हैं। इसके लिए शीट के एक और एक छोटा बेलनाकर गाउसीएन पृष्ठ लेते हैं जिसमें तीन पृष्ठ होते हैं, दो सपाट flate surface पृष्ठ एवं तीसरा तिर्यक पृष्ठ curved surface, 

यह भी पढ़े

• 📂Coulomb Law कूलाम्ब का नियम
• 📂आवेश के गुण Properties Of Charge
• 📂 विद्युत क्षेत्र Electric Field Intensity
• 📂 विद्युत बल रेखायें Electric Field Line
• 📂 विद्युत द्विध्रव Electric Dipole Moment
• 📂 विद्युत द्विध्रुव पर बल आघूर्ण 
• 📂 विद्युत flux Electric Flux
• 📂 Gauss Law गाउस का नियम
• 📂 Application Of Guass Law
• 📂 Class 11th Physics

     बेलनाकार पृष्ठ पर आवेश सममित है। आपको नीचे चित्र में स्पष्ट रूप से दिखाई दे रहा होगा कि पृष्ठ A व B  पर विद्युत क्षेत्र की तीव्रता क्रमशः E1 व E2 हैं।

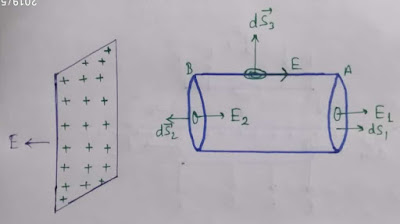electric field due to non conducting sheet in hindi, आवेशित अचालक शीट के कारण विद्युत क्षेत्र की तीव्रता

सपाट पृष्ठ A पर विद्युत क्षेत्र E1 तथा सूक्ष्म सदिश क्षेत्रफल dS1 के बीच बनने वाला कोण =0°
पृष्ठ A से होकर जाने वाला विद्युत फ्लक्स electric flux

      φ1 = ∫E1·dS1 = ∫E1dS1cos 0°

      ≡ E∫dS1 = E1a       [∵∫dS1 = a]

पृष्ठ B पर विद्युत क्षेत्र E2 तथा सूक्ष्म क्षेत्रफल dS2 के बीच बनने वाला कोण = 180°

 ∴  सपाट पृष्ठ B से होकर जाने वाला फ्लक्स electric flux

       φ2 = ∫E2·dS2 = ∫E2dS2cos 180°

      ≡ -E∫dS2 = -E2a       [∵∫dS2 = a]

तिर्यक पृष्ठ के प्रत्येक बिंदु पर विद्युत क्षेत्र की तीव्रता E तथा वक्र पृष्ठ dS3 क्षेत्रफल के बीच बनने वाला कोण = 90°

∴ तिर्यक पृष्ठ से होकर जाने वाला विद्युत फ्लक्स electric flux

        φ3 = ∫E3·dS3  = ∫E3dS3cos90°  = 0                           [∵cos90° = 0]

∴ बेलनाकार पृष्ठ से होकर जाने वाला कुल विद्युत फ्लक्स electric flux

     φ(total) = φ1+ φ2 + φ3

  = E1a - E2a + 0 = ( E1 - E2)a      ...... (1)

क्योंकि पृष्ठ सीट के एक तरफ है अतः पृष्ठ द्वारा घिरा आवेश = 0 (zero)

गाउस प्रमेय से बेलनाकार पृष्ठ sylindrical surface से होकर जाने वाला कुल विद्युत फ्लक्स electric flux

           φ(total) = 1/ε×(0) = 0.    (2)

समीकरणों (1) व (2) की तुलना करने पर

           (E1 - E2)a = 0

           अतः   E1 = E2

इससे स्पष्ट है कि सीट के निकटवर्ती सभी बिंदु पर विद्युत क्षेत्र की तीव्रता समान है अर्थात.  E1 = E2 = E


Also Read:-

◆अनंत लंबाई के आवेशित तार के निकट विद्युत क्षेत्र की तीव्रता

◆Important Fact of Gauss law

◆Graphical Representation Of Motion,X-T And V-T Graph

आवेशित अचालक सीट से r दूरी पर स्थित किसी बिंदु पर विद्युत क्षेत्र का मान (Electric field due to non conducting sheet at r distance ):-

   अब हमें शीट sheet के निकट r दूरी पर विद्युत क्षेत्र electric field की तीव्रता intensity ज्ञात करनी है, इसके लिए हम पहले ही यह देख चुके हैं की सीट के निकट प्रत्येक बिंदु पर विद्युत क्षेत्र की तीव्रता का मान समान होता है।

        इस प्रकार हम इस शीट के कारण विद्युत क्षेत्र था की तीव्रता निकालने के लिए एक गाऊसीयन बेलनाकार पृष्ठ gausian sylindrical surface इस प्रकार लेते हैं कि इसके flat surface सपाट पृष्ठ सीट के दोनों ओर स्थित हों अर्थात यदि सीट को बेलनाकार पृष्ठ के बीच रखा जाए तथा curved surface तिर्यक पृष्ठ सीट के लंबवत हो जो कि शीट को काटकर जाता हो

  आपको नीचे चित्र में भलीभांति दिख रहा होगा कि कैसे सीट बेलनाकार गौसियन पृष्ठ को काट कर जाती है।
    इस गाउसियन पृष्ठ को तीन भागों में divided विभाजित किया जा सकता है

(1)दाएं और का वृत्ताकार पृष्ठ S1 right side

(2) बाएं और का का वृत्ताकार पृष्ठS2 left side

(3)  बेलनाकार पृष्ठ S3 curved surface side

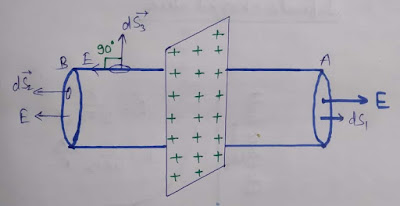electric field due to non conducting sheet in hindi

Also Read:-
◆महाराणा प्रताप से जुड़े अनोखे तथ्य
◆वीर सावरकर के बारे में रोचक तथ्य
◆जानिए भारत का भूगोल

अब E व dS1 के बीच बनने वाला कोण = 0°

∴ पृष्ठ A से होकर जाने वाला विद्युत फ्लक्स

 φ1 = ∫E·dS1 = ∫E·dS1cos 0° = Ea ......(1)

E व dS2 के बीच बनने वाला कोण = 0°

∴ पृष्ठ B से होकर जाने वाला विद्युत फ्लक्स,

φ2 = ∫E·dS2 = ∫E·dS2cos 0° = Ea   .....(2)

      [ a = पृष्ठ का क्षेत्रफल area of surface ]

तिर्यक पृष्ठ से होकर जाने वाला विद्युत फ्लक्स,

 φ3 = ∫E·dS3 = ∫E·dS3cos 90° = 0    ....(3)

∴ बेलनाकार पृष्ठ से होकर जाने वाला कुल विद्युत फ्लक्स

        φ =  φ1 + φ2 + φ3   

         = Ea + Ea + 0 = 2Ea         …...(4)

पृष्ठ द्वारा घिरा कुल आवेश = σa

गौस की प्रमेय से पृष्ठ से होकर जाने वाला कुल विद्युत फ्लक्स

                = 1/ε×(σa)       .....(5)

समीकरणों (4) व  (5) की तुलना करने पर

                2Ea = 1/ε×(σa)

             ⇒      E = σ/2ε

विद्युत क्षेत्र का यह सूत्र पृष्ठ से दूरी r पर निर्भर नहीं करता है।

   इससे यह स्पष्ट हो जाता है कि सीट के निकट सभी बिंदु पर विद्युत क्षेत्र की तीव्रता का Magnitude परिमाण समान होता है, तथा इसकी दिशा धनआवेशित सीट के अभिलंब शीट से बाहर की ओर होगी जबकि ऋण आवेशित शीट के कारण यह शीट की ओर होगी।

यह भी पढ़े

• 📂Coulomb Law कूलाम्ब का नियम
• 📂आवेश के गुण Properties Of Charge
• 📂 विद्युत क्षेत्र Electric Field Intensity
• 📂 विद्युत बल रेखायें Electric Field Line
• 📂 विद्युत द्विध्रव Electric Dipole Moment
• 📂 विद्युत द्विध्रुव पर बल आघूर्ण 
• 📂 विद्युत flux Electric Flux
• 📂 Gauss Law गाउस का नियम
• 📂 Application Of Guass Law
• 📂 Class 11th Physics

Tag:- gauss law applcation, gauss law in hindi, electrical Field, gausian surface, intensity of electric Field , Electric Flux in Hindi, gauss law derivation, gauss theorem in hindi class,electric field due to non conducting sheet, electric field due to infinite conducting sheet of charge, electric field due to conducting sheet, electric field due to infinite sheet of charge derivation, electric field due to finite sheet of charge



           अगर आपकोgauss law Application के बारे में जानकारी अच्छी लगती है तो हमें Comment में जरूर बताएं एवं इस post को अपने दोस्तों तक जरूर Share करें।