Application of Gauss law
gauss law applcation, electric field due to infinite line charge derivation, gauss law in hindi
गाउस का नियम सममिति आवेश वितरण Symmetrical distribution of charged की स्थिति में उत्पन्न विद्युत क्षेत्र electrical Field की तीव्रता की गणना के लिए प्रयोग किया जाता है इसके लिए एक ऐसा बंद पृष्ठ चुनते हैं जिसके विभिन्न फलकों facese पर विद्युत क्षेत्र या तो फलक के समांतर हो या लंबवत हो इस बंद पृष्ठ को गाउसियन पृष्ठ gausian surface कहते हैं। गौशियन पृष्ठ किसी भी आकृति shape का हो सकता है जैसे गोलाकार spherically, बेलनाकार sylindrical या कोई अन्य आकृति का हो सकता है।
इस आर्टिकल article में आपको अनंत लंबाई infinity length के आवेशित तार charge wire के निकट विद्युत क्षेत्र की तीव्रता intensity of electric Field की गणना करके दिखायेंगे।
Electric field strength near an infinite charged wire अनंत लंबाई के आवेशित तार के निकट विद्युत क्षेत्र की तीव्रता:-
माना एक तार एक charged uniformly distributed समान रूप से आवेशित है, तो तार की प्रति एकांक लंबाई per unit length पर आवेश को रेखीय आवेश घनत्व (linear charged density) कहते हैं यदि L लंबाई की तार पर आवेश Q हो, तो रेखीय आवेश घनत्व linear charged density = Q/Lयह भी पढ़े
- 📂Coulomb Law कूलाम्ब का नियम
- 📂आवेश के गुण Properties Of Charge
- 📂 विद्युत क्षेत्र Electric Field Intensity
- 📂 विद्युत बल रेखायें Electric Field Line
- 📂 विद्युत द्विध्रव Electric Dipole Moment
- 📂 विद्युत द्विध्रुव पर बल आघूर्ण
- 📂 विद्युत flux Electric Flux
- 📂 Gauss Law गाउस का नियम
- 📂 Application Of Guass Law
- 📂 Class 11th Physics
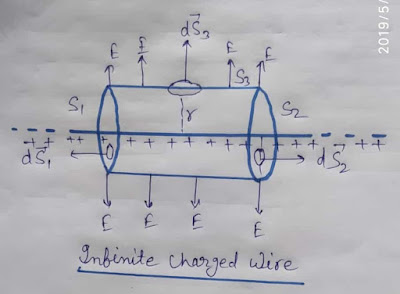
मान लेते हैं कि हमारे पास एक अनंत लंबाई का आवेशित तार charged wire है जिसका रेखीय आवेश घनत्व linear charged density (λ Columbus/meter) इससे r दूरी पर एक बिंदु है जिस पर विद्युत क्षेत्र की तीव्रता का मान ज्ञात करना है माना r त्रिज्या तथा l लंबाई का एक बेलनाकार गौसियन पृष्ठ है बेलन में 3 पृष्ठ होते हैं दो सपाट पृष्ट S1, व S2 व तीसरा वक्र पृष्ट S3,
नीचे चित्र की भांति आपको दिखाया गया है कि किस प्रकार बेलनाकार पृष्ठ से विद्युत क्षेत्र की तीव्रता की दिशा तथा प्रत्येक पृष्ठ की दिशा किस प्रकार है।
 |
| Application of Gauss law |
विद्युत क्षेत्र E तथा S1 के किसी लघु पृष्ठ क्षेत्रफल dS1 के बीच बनने वाला कोण = 90°
पृष्ठ S1 से होकर जाने वाला विद्युत फ्लक्स φ.
φ1 = ∫E·dS1 = ∫E·dS1cos 90° = 0
विद्युत क्षेत्र E तथा S2 के किसी लघु पृष्ठ क्षेत्रपल dS2 के बीच बनने वाला कोण = 90°
अतः पृष्ट S2 से होकर जाने वाला कुल विद्युत फ्लक्स,
φ2 = ∫E·dS2 = ∫E·dS2cos 90° = 0
Aso read
◆गाउस का नियम:-Gauss law in hindi,
◆Electric Flux in Hindi
◆Coulomb's Law)
विद्युत क्षेत्र E तथा S3 के किसी छोटे पृष्ठ dS3 के बीच बननेवाला कोण = 0°
∴ पृष्ठ S3 से होकर जाने वाला कुल विद्युत फ्लक्स,
φ3 = ∫E·dS3 = ∫E·dS3cos 0°
= E∫dS3 = E·2πrl
[dS3 = बेलनाकार वक्र पृष्ठ का क्षेत्रफल = 2πrl]
∴ बेलनाकार पृष्ठ से होकर जाने वाला कुल विद्युत फ्लक्स
φ(total) = φ1 + φ2 + φ3 = 0 + 0 + E·2πrl
बेलनाकार पृष्ठ द्वारा घिरा कुल आवेश = λl
गॉस की प्रमेय से बेलनाकार पृष्ठ से होकर जाने वाला कुल विद्युत फ्लक्स
φ(total) = Q/ε = 1/ε(λl)
समीकरण (1) व (2) से
E·2πrl = 1/ε(λl)
E = λ/2πεr अथवा E = 1/4πε(2λ/r)
 |
| Application of Gauss law |
इस प्रकार रेखीय आवेश के कारण विद्युत क्षेत्र की तीव्रता रेखीय आवेश से बिंदु की दूरी (r) के व्युत्क्रमानुपाती होती है तथा इसकी दिशा रेखीय आवेश के लंबवत बाहर की ओर होती है।
अर्थात किसी बिंदु पर विद्युत क्षेत्र की तीव्रता उसकी तार से दूरी के व्युत्क्रमानुपाती होता है।
एक आवेशित बेलनाकार चालक, बाह्य बिन्दुओ के लिए ऐसे व्यवहार करता है जैसे कि संपूर्ण आवेश इसकी अक्ष पर स्थित हो।
यह भी पढ़े
- 📂Coulomb Law कूलाम्ब का नियम
- 📂आवेश के गुण Properties Of Charge
- 📂 विद्युत क्षेत्र Electric Field Intensity
- 📂 विद्युत बल रेखायें Electric Field Line
- 📂 विद्युत द्विध्रव Electric Dipole Moment
- 📂 विद्युत द्विध्रुव पर बल आघूर्ण
- 📂 विद्युत flux Electric Flux
- 📂 Gauss Law गाउस का नियम
- 📂 Application Of Guass Law
- 📂 Class 11th Physics
अगर आपको gauss law Application के बारे में जानकारी अच्छी लगती है तो हमें Comment में जरूर बताएं एवं इस post को अपने दोस्तों तक जरूर Share करें।

Post a Comment
Post a Comment